从本质上说，在众多可交割券中，只有CTD券才是国债期货的标的资产。作为国债期货的定价和套期保值的基准，CTD券很自然地成为国债期货市场关注的焦点。问题在于，国债期货到期之前，哪个券是真正的CTD券，是无法预知的。人们只能退而求其次，选择当时的信息条件下最可能成为未来CTD券的“准CTD券”，作为定价和套期保值的基准。

　　那么，如何判断“准CTD券”呢？

　　一般公认，给定时刻IRR（Implied Repo Rate，隐含回购利率）最大的券就是当时条件信息下的最合算债券；但也有人认为择券期权价值最小的债券是“准CTD券”；与之相关的概念还有基差、BNOC等。本文对这些概念进行深入的辨析，希望能为这一问题提供答案，为实际操作提供参考。

　　一、隐含回购利率（IRR）准则

　　我们首先对最广泛使用的“准CTD券”标准——隐含回购利率（IRR）进行分析。如果期货剩余期限内没有遇到债券付息日，债券i的IRR被定义为：

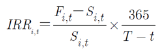　　(1)

　　其中F_i,t和S_i,t分别为t时刻的可交割券i的期货全价（即按照t时刻的期货价格交割所收到的全部现金）和可交割券i的现货全价。

　　可以看出，对期货空方来说，IRR_i,t实际上是这样一种“持有到期策略”的年化收益率：在t时刻购买1单位现券i，同时卖空同样数量的国债期货，然后将可交割券i持有到期货到期T时刻进行交割，到期卖价锁定为t时刻的期货价格。债券在t时刻的IRR最大意味着年化收益率最大，从而是t时刻条件信息下的最合算债券。

　　从这里也可以看出，如果IRR_i,t高于t时刻交易者的资金成本，理论上就存在套利机会：借钱买入现券，卖出期货，锁定收益率为IRR，而资金成本相对较低，可以获得套利利润。因此在无套利情况下，IRR_i,t应等于t时刻的资金成本。由于金融机构的短期资金成本多为回购利率，IRR（隐含回购利率）因此而得名。

　　如果就此来看，以IRR作为t时刻信息条件下判断“准CTD券”的标准，似乎是合理的。然而，现实并不这么简单。在很多情况下，可交割券在期货剩余期限内都会遇上付息日。一般的处理是，将式(1)拓展为：

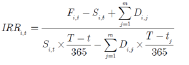　　(2)

　　其中，m表示期货剩余期限内现券i派息的次数，t_j表示该券派息的时刻，D_i,j表示面值为100元的债券第j次派息支付的利息金额。可以看出，如果期货剩余期限内不付票息，D_i,j为0，式(2)就退化为式(1)。

　　尽管在无付息的情形下，式(1)用于判断“准CTD券”基本没有问题；但若期货剩余期限内债券派息，式(2)事实上做了一个重要的假定：这些派息未来一定能够按照IRR_i,t进行再投资。因为式(2)是由下式得到的：

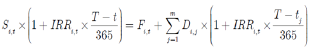　　(3)

　　式(3)的含义是：购买现券所占用的资金按照IRR_i,t进行投资的回报等于约定期货的卖价与票息按IRR_i,t进行再投资的加和。由于在t时刻我们无法保证未来的派息一定能够按照IRR_i,t进行再投资，所以式(2)显然并不精确。换言之，式(2)中这个被用于作为“准CTD券”判断标准的IRR实际上是无法实现的。

　　事实上，只要对式(3)略加修改，我们就可以得到一个可实现的隐含回购利率 ：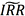

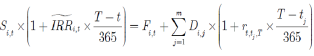　　(4)

　　其中r_t,tj,T表示t时刻的远期利率，远期期限为T-t_j。也就是说，可以运用远期利率协议或类似工具将未来派息的再投资收益锁定。相应的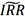计算公式为：

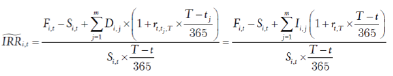　　(5)

　　其中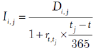

　　我们认为，由于其策略的可实现性，以式(5)定义的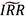最大的债券作为t时刻条件信息下的最合算债券，会比原始的IRR标准更为合理。相应的套利可行性判断准则应改为：如果以式(5)定义的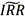高于t时刻交易者的资金成本，理论上就存在套利机会。此时借钱买入现券，卖出期货，并用远期利率协议将未来派息的再投资收益锁定，就可以保证投资收益率为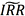，而资金成本相对较低，从而获得套利利润。

　　进一步看，我们还可以得到一个基于原始IRR的新的套利可行性判断准则：

　　如果对于给定的可交割券，对任意时刻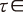{t₁,t₂,…,t_m,T}，均有IRR_i,t≥r_t,τ，且等号不全成立，则对该可交割券执行“持有到期策略”可以套利。其中t_j{t₁,t₂,…,t_m}表示期货剩余期限内的该可交割券的派息时刻，r_t,τ表示t时刻期限为τ-t的即期利率。

　　对式(3)和式(4)略作变换，可以很容易地证明以上准则。引入一个变量：

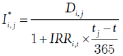　　(6)

　　注意，式(6)中的I^*_i,j是未来t_j时刻债券派息金额D_i,j以原始IRR贴现的现值，而式(5)中的I_i,j则是D_i,j以当前t到t_j时刻无风险利率贴现的现值。将这两个变量分别代入式(3)和式(4)，可以得到：

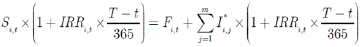　　(7)

　　和

　　(8)

　　如果对任意{t₁,t₂,…,t_m,T}，均有IRR_i,t≥r_t,τ，且等号不全成立，意味着：

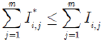
　　进一步有，

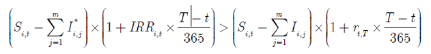
　　代入式(6)和式(7)，我们发现

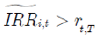
　　从而存在套利机会。

　　从理论上来说，和原始IRR相比，使用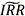作为“准CTD券”的判断准则显然更为合理。从上述讨论中也可发现，无论IRR准则如何改善，其本质上只是刻画了一种在t时刻条件信息下严格执行“持有到期”这一特定策略所得到收益最高的债券特征，与该债券未来是否成为真正的CTD券并无严格的关联。虽然从投资策略的角度来说将IRR或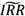作为“准CTD券”的判断准则有一定的合理性，但并非是完美的。

　　二、择券期权价值的定义

　　除了IRR准则之外，实际操作中另一个判断“准CTD券”的准则是：具有最低择券期权价值的可交割券是“准CTD券”。为分析这一准则是否合理，需要对择券期权及其价值的内涵作深入分析。

　　国债期货本质上仍是期货，只是由于其额外赋予期货空方在到期交割时选择CTD券的权利，因而隐含了一个择券期权。因此择券期权价值可以由不含权的国债期货价格与含权的国债期货价格之差计算得到。具体分析如下：

　　对于任意的可交割券i，假设市场上存在以单只可交割券i为标的资产的期货合约，由于这个期货合约不含期权，其定价与普通期货的定价无异，可以用“持有成本法”定价：

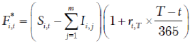　　(9)

　　也就是说，不含权的可交割券i的期货全价等于其现券全价S_i,t减去期货存续期间内债券派息的现值，再以无风险利率计算得到的终值。

　　如果考虑择券期权，由于对空方有利而对多方不利，这一期权的存在必然会反映在国债期货价格中，使得国债期货价格相对下降。因此含权的国债i的期货全价为：

　　(10)

　　其中f_i,t表示t时刻，与期货全价所对应的可交割券i的择券期权的价值（严格来说，还需对f_i,t进行从T时刻到t时刻的贴现，才能得到真正经济学意义上t时刻的择券期权价值，但在国债期货的定价中，人们关心的是这一期权价值对期货价格的影响，由于期货价格是现货价格的无风险终值，这样贴现与计算终值相互抵消，期货价格中的择券期权价值正好是f_i,t）。

　　当然，根据国债期货合约的规定，最后交易时使用的价格应是标准券期货的净价。因此得到含权的可交割券i的期货全价F_i,t之后，还需要进行以下两个转换：先减去可交割券i在期货交割日的应计利息AI_i,T得到净价，再除以该券的转换因子CF_i，得到对应的标准券期货净价，才是最终在交易中使用的国债期货报价。具体公式为：

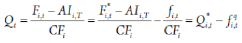　　(11)

　　其中

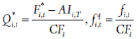　　(12)

　　式(11)中的Q_t为t时刻考虑择券期权的标准券期货的报价，Q^*_i,t为不含权的标准券期货的理论报价，f^q_i,t则为与标准券期货报价所对应的可交割券i的择券期权价值。可以看出，t时刻f^q_i,t最小的债券，就是不含权国债期货报价Q^*_i,t和真实国债期货报价Q_t之间差距最小的可交割券。

　　三、国债期货的基差、净基差（BNOC）与择券期权价值

　　在国债期货交易中，基差（Basis）和净基差（Basis Net of Carry，BNOC）是非常常见的概念。它们与择券期权价值之间也存在着联系。

　　对于可交割券i，其t时刻的基差被定义为：

　　(13)

　　也就是现券净价P_i,t减去标准券期货报价Q_t同该券转换因子的乘积。

　　而t时刻现货净价等于t时刻现货全价减去t时刻应计利息，即

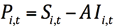
    同时，根据式(9)至(11)，可以得到

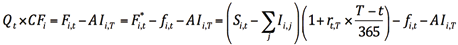
　　代入基差的计算公式(13)，可以发现债券基差可以分解为持有收益（Carry）和择券期权价值之和：

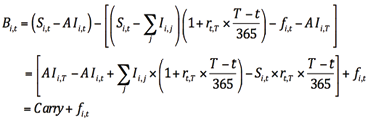　　(14)

　　其中Carry就是从t时刻到期货到期的T时刻，持有现券多头和期货空头组合的持有期收益，等于该期间的票息收入和派息再投资收入之和减去购买现券所承担的资金成本。

　　式(14)表明，对于任意的可交割券，只要用现券净价和标准券期货报价、转换因子等市场信息计算出基差，然后减去相应的持有期收益，就可以得到市场隐含的该债券对应的择券期权价值。但人们通常称其为t时刻该券的“净基差”（Basis Net of Carry，BNOC，即基差减去持有期收益），只有t时刻的“准CTD券”所对应的BNOC才被称为“隐含的择券期权价值”。

　　值得注意的是，基差的大小和BNOC并不完全同步变化，因为其中还包括持有收益的部分。

　　四、择券期权价值准则及其与IRR准则的关系

　　从直觉上说，择券期权价值越小，被换券的可能性就越小，因此择券期权价值最小常常也被作为“准CTD券”的判断标准。那么这一准则是否准确合理？它与IRR准则又是何关系呢？

　　尽管初看之下颇为合理，但正如Burghardt（2005）指出的，由于不同可交割券的现货价格一般是不同的，在选择不同可交割券进行交割时，空方所投入的本金通常也是不同的，直接使用择券期权价值进行排序只考虑了交易收益的绝对金额，而没有考虑收益率，因此仍然不够合理。

　　如果我们对其加以改进，考虑其初始成本S_i,t，则择券期权价值最小准则可以改进为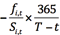最大，即年化择券期权收益率最小准则。我们很快可以发现，这与本文所提出的改进后的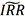最大准则具有内在一致性。简单推导如下：

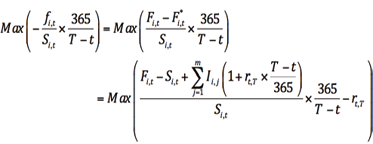　　(15)

　　而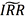最大准则为

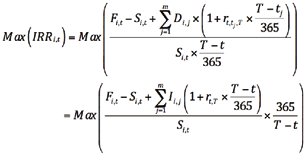　　(16)

　　对比式（15）和（16），显然择券期权收益率准则的核心与一致，但进一步扣减了购买现券所需的资金成本。如果投资者在所有可交割券上的资金成本都一样，择券期权收益率准则与准则就完全相同；但如果投资者在不同券上的资金成本不同（在某些券相对紧缺时，市场常出现这种情形），显然择券期权收益率准则更为合理和准确。

　　五、结论

　　改进后的“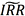准则”和“择券期权收益率准则”在本质上具有内在一致性，但择券期权收益率准则由于考虑了初始资金成本，是相对更优的标准。也就是说，只要运用期货、现货净价和持有期收益（carry）计算得到BNOC，再除以债券现货价格，得到的择券期权收益率较小者，就是t时刻条件信息下的CTD券。当然，由于都是t时刻条件信息下的结论，无论原始准则还是改进准则，都与该债券未来是否成为真正的CTD券并无完全严格的关联。

　　需要说明的是，本文提出的仅是理论上的“准CTD券”的判断准则。在实际市场中，往往会出现与理论不一致的情形。例如，在中国市场上，当日符合“准CTD券”选择准则的债券不一定能买到，或不一定能按照看到的市场价格成交。另一种在中国市场上出现的常见情形则是，虽然从理论上说，符合准则的债券改变了，但市场可能整体存在一定的惯性，或存在一定的换券成本，或不同市场的参与者对可交割券存在不同的偏好，使得市场不会轻易改变之前对“准CTD券”的判断，即市场对“准CTD券”选择并非完全理性。这两种情形都有可能使得上述“准CTD券”的判断准则失效。

　　因此，在实际操作中，通常还需要结合市场流动性以及市场惯性等方面进行综合分析。一种可行的做法是：先运用“择券期权收益率”等准则进行排序，而后根据市场的流动性、债券可得性和市场的惯性来判断当日的“准CTD券”。

　　（陈蓉系厦门大学金融系教授，葛骏系厦门大学金融系金融工程博士生；本文得到国家自然科学基金资助，项目编号为：71371161和71471155）